Riemann-Hilbert theory and nonlinear connection problems

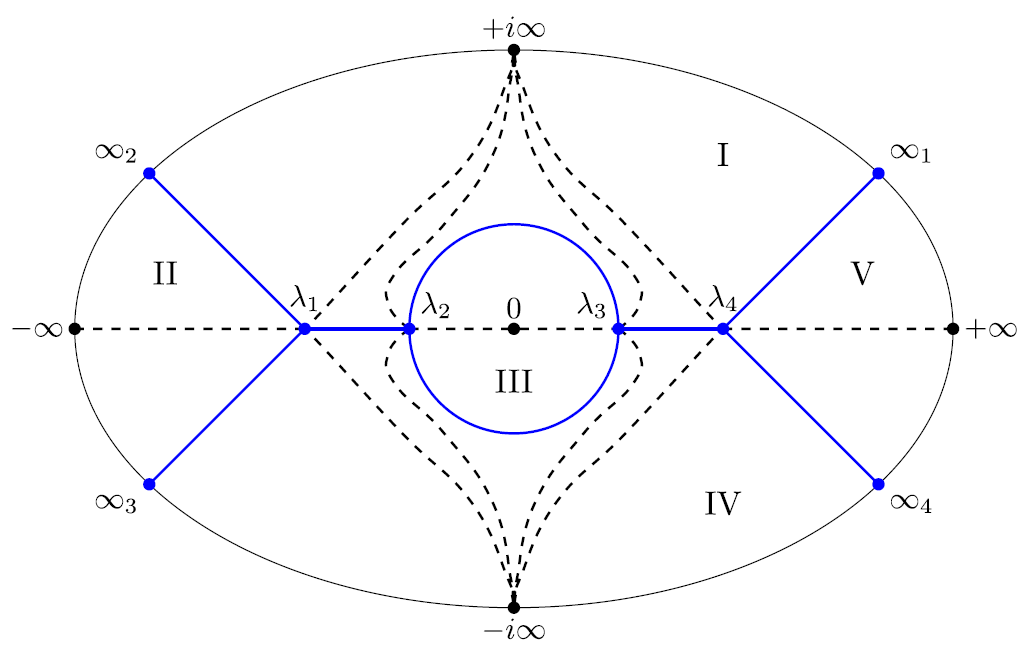
One of the ultimate manifestations of integrability in nonlinear equations is the possibility to solve connection problems between different critical points. In my PhD thesis, I studied the connection problem of a q-difference Painlevé equation and derived an implicit solution that relates the asymptotic behaviours of solutions near t=0 to the asymptotic behaviours of solutions near t=∞. In a recent publication in Nonlinearity, I used a Riemann-Hilbert approach to solve the connection problem for the q-Painlevé VI equation and showed that it is related to the beautiful geometry of some classical algebraic surfaces known as Segre surfaces.

From left to right: Orbit of Kaneko-Ohyama points, Geometric visualisation of a Mano decomposition, Clebsch graph that encodes intersections among lines.

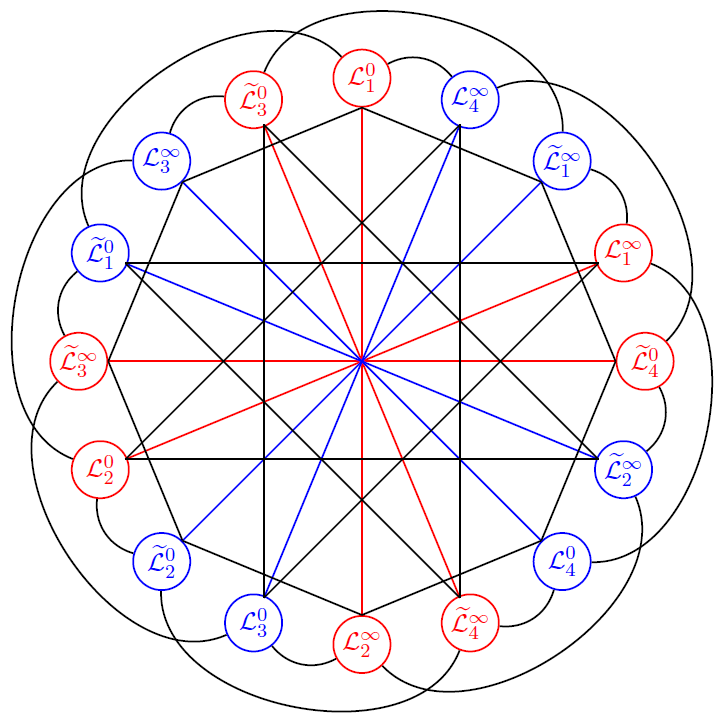
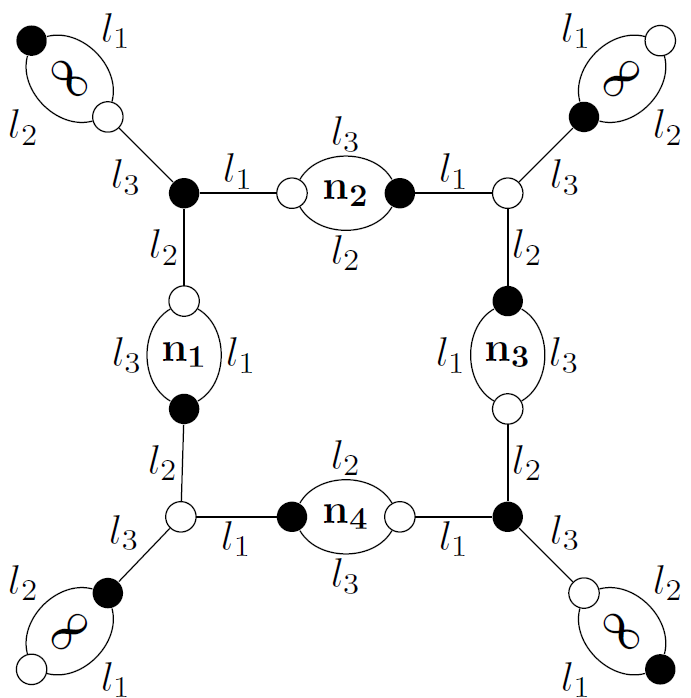
Geometry of affine Segre surfaces and Painlevé equations

In a recent collaboration together with Marta Mazzocco and Nalini Joshi, we study a six-dimensional family of affine Segre surfaces whose generic members are associated with the q-difference sixth Painlevé equation. We derive a reduction of this family under the continuum limit q→1, and relate the resulting Segre surface explicitly to the celebrated Jimbo-Fricke cubic surface. Following the confluence diagram of Painlevé equations, we then obtain Segre surfaces for each of the (unramified) differential Painlevé equations.

Intersection diagram of affine lines on the Jimbo-Fricke cubic surface and in red a Clebsch subgraph that encodes intersections among lines on an associated Segre surface.

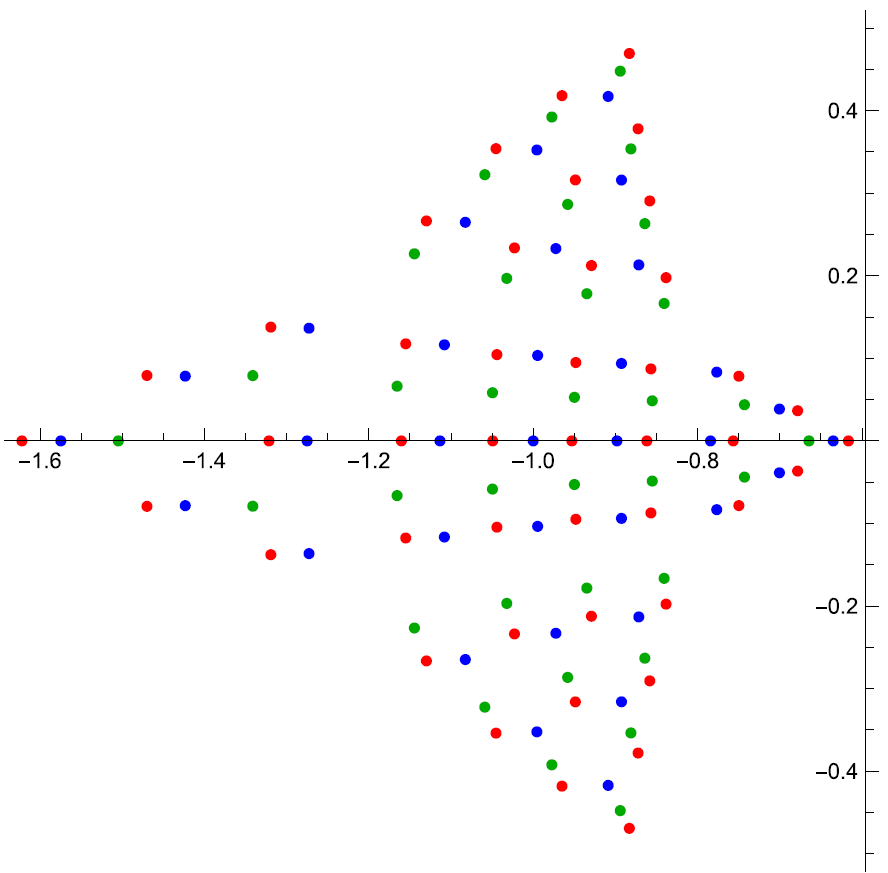
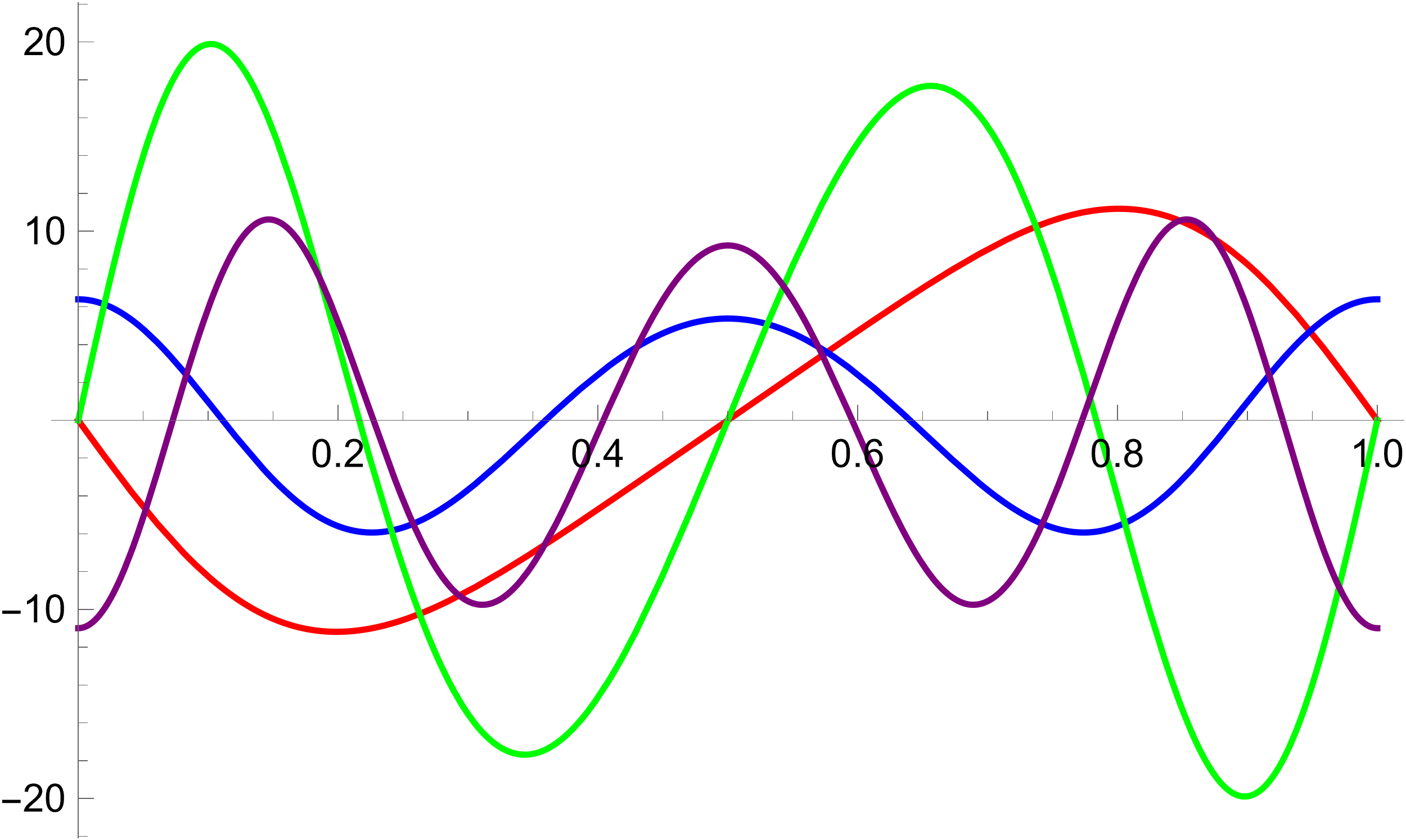
Quantisation, value distributions and Nevanlinna theory

Together with Davide Masoero, I have been studying value distributions of Painlevé functions through a correspondence with quantisation problems of Heun equations. In our first paper, we classified zeros of Wronskians of Hermite polynomials in terms of certain branched coverings of the Riemann sphere using a theory developed by Nevanlinna. We further derived their asymptotic distribution whilst the size of the Wronskians remains bounded. In our second paper, we worked out the unrestricted asymptotic distribution of the zeros as the degree of the polynomials grows large, using a complex WKB approach.

From left to right: Stokes and anti-Stokes complices, deformed rectangular grid with zeros superimposed, dessin d'enfants corresponding to zeros of generalised Hermite polynomials.

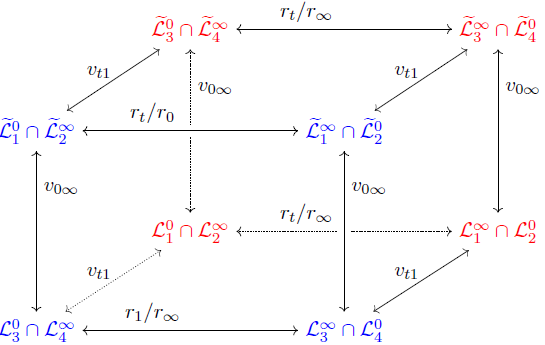
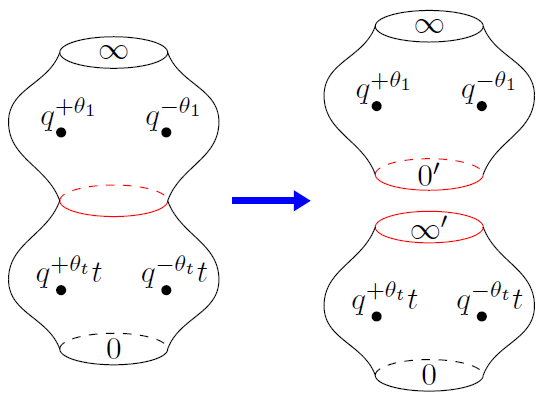
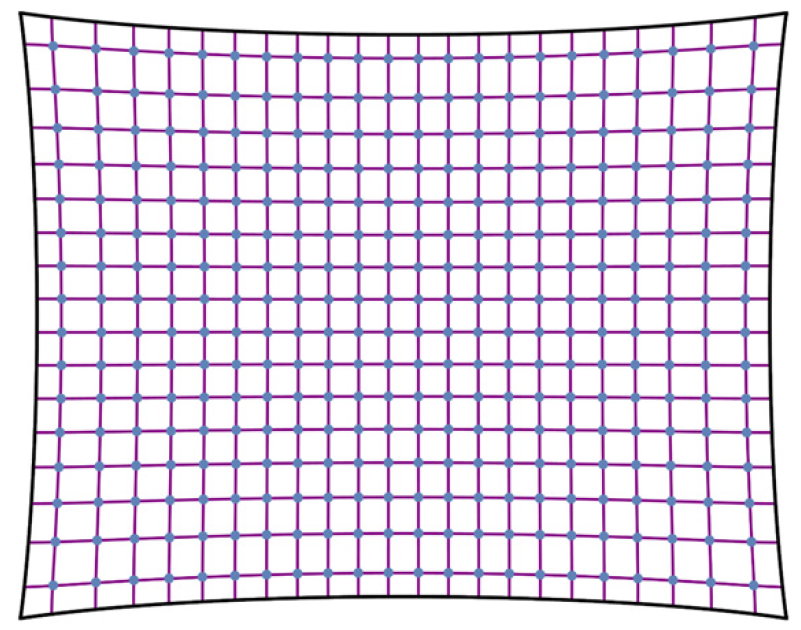
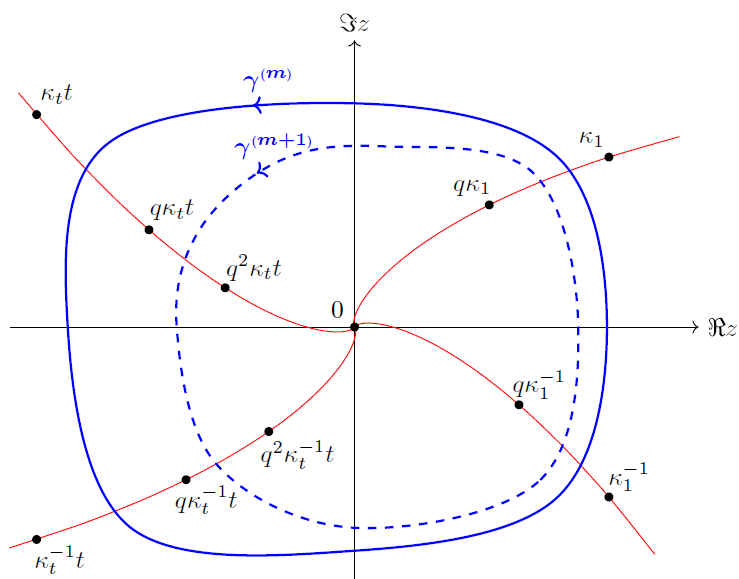
Monodromy manifolds and q-difference equations

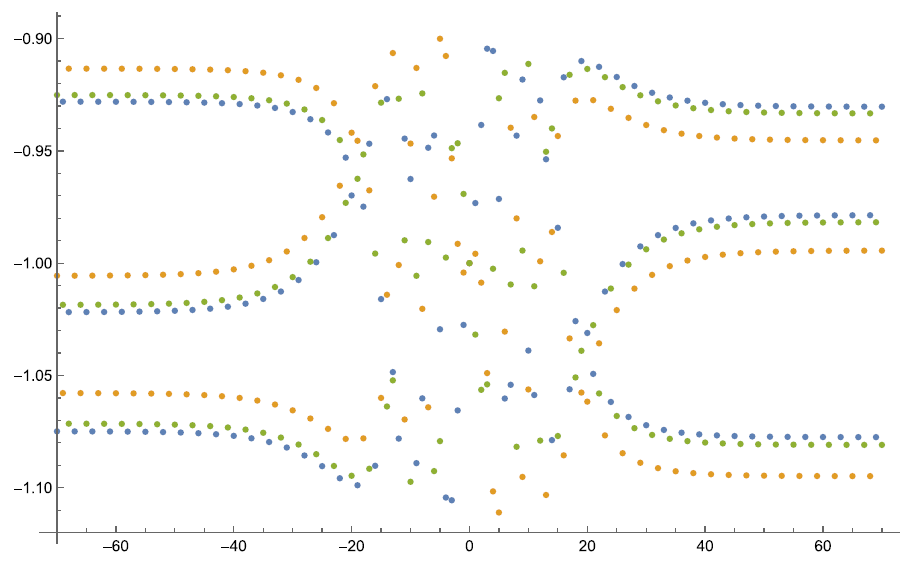
Together with Nalini Joshi, I have been working on the construction of monodromy manifolds for q-difference equations and corresponding Riemann-Hilbert problems. In our first paper on this topic published in CMP, we constructed a monodromy manifold for q-Painlevé IV and identified it with a hypersurface in (CP^1)^3 and further showed that the corresponding Riemann-Hilbert problem is solvable. In a follow-up paper, we used this framework to study symmetric solutions of q-Painlevé IV. We then constructed a monodromy manifold for q-Painlevé VI, which was also published in CMP. In this case, the monodromy manifold is a Segre surface. We further showed that, for special values of the parameters, this surface is singular and the singularities correspond to those cases where the Riemann-Hilbert problem can be solved exactly in terms of orthogonal polynomials.

From left to right: poles of symmetric solutions, contour of the Riemann-Hilbert problem for q-Painlevé VI, plot of a symmetric solution of q-Painlevé IV.

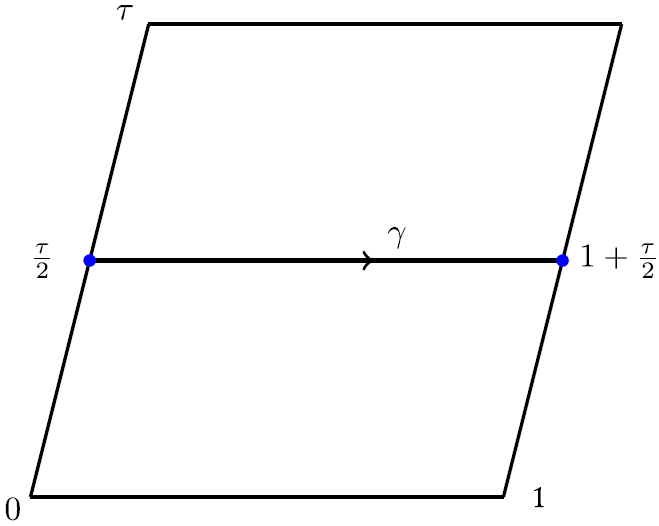
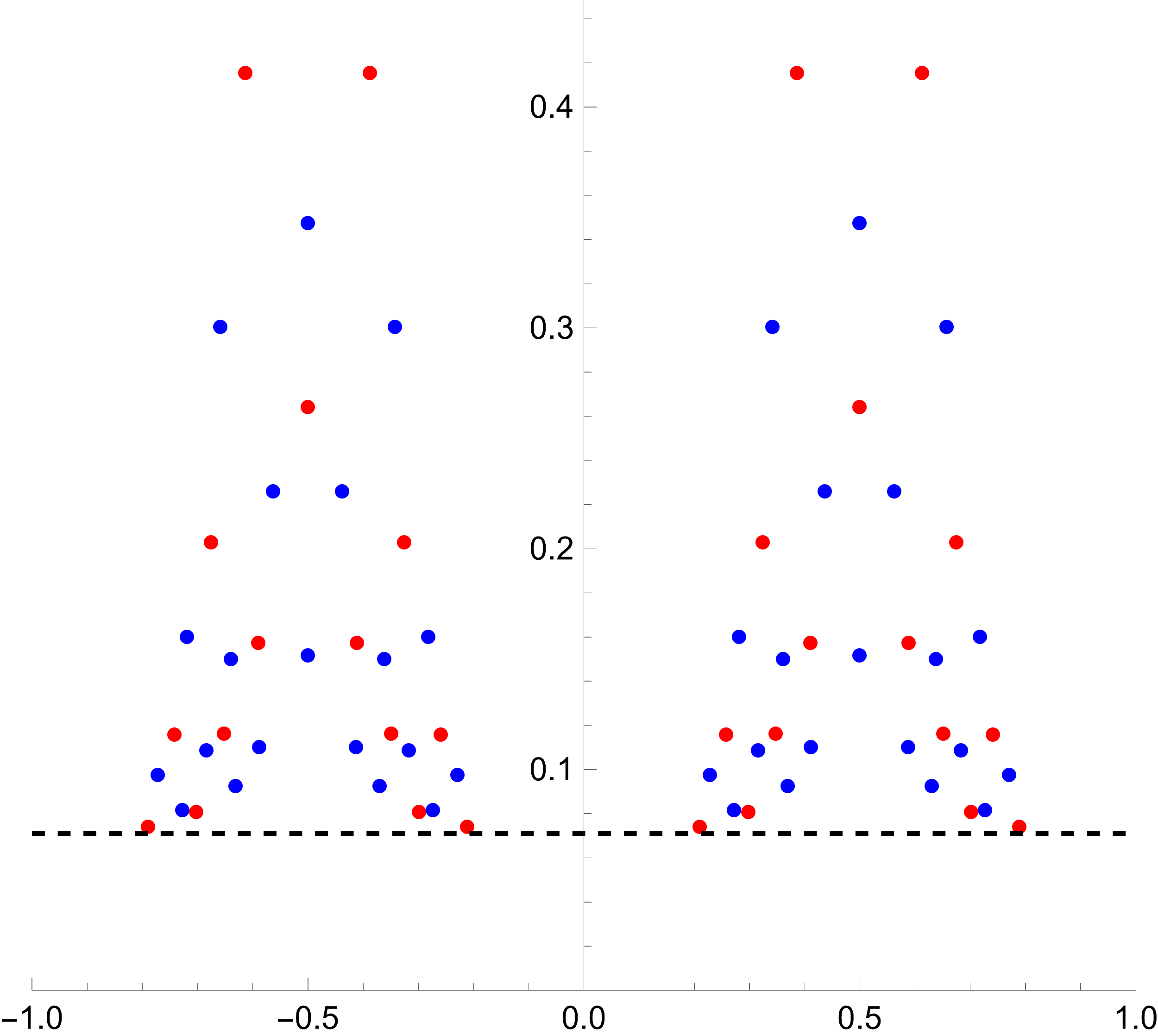
Orthogonal polynomials on elliptic curves

In a recent collaboration with Harini Desiraju and Tomas Latimer, we introduced a new class of orthogonal polynomials on elliptic curves and studied their integrability.

From left to right: torus with support of weight function, plots of some of the orthogonal polynomials on support, zeros of the Hankel determinant of moments in the upper half-plane.